বাইনারি থেকে দশমিক আমরা বাইনারি সংখ্যাকে দশমিক সংখ্যায় এবং দশমিক সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর করতে পারি। নিচে বাইনারি সংখ্যাকে দশমিক সংখ্যায় রূপান্তর করার আরেকটি উদাহরণ দেয়া হলো।1011012=1×25+0x24+1×23+1×22+0x21+1×20=32+0+8+4+0+1=4510দশমিক থেকে বাইনারিঠিক একইভাবে একটি দশমিক সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর করতে হলে দশমিক সংখ্যাটিকে প্রথমে 2-এর পাওয়ারের যোগফল হিসেবে লিখতে হবে। যেরকম:76 = 64+8+4=26+23+22বাইনারি সংখ্যায় যেহেতু স্থানীয় মান রয়েছে তাই প্রত্যেকটি স্থানীয় মানকে দেখাতে হবে। যেগুলো নাই তার জন্য 0 ব্যবহার করতে হবে।7610 = 26+0+0+23+22+0+0=10011002তবে যে কোনো সংখ্যাকে 2-এর পাওয়ারের যোগফল হিসেবে বের করার একটি সহজ উপায় হচ্ছে ক্রমাগত 2 দিয়ে ভাগ করে যাওয়া। যতক্ষণ পর্যন্ত ভাগফল শূন্য না হবে ততক্ষণ পর্যন্ত 2 দিয়ে ভাগ করে যেতে হবে। ভাগশেষগুলো LSD থেকে শুরু করে ক্রমান্বয়ে MSB পর্যন্ত বাইনারি সংখ্যাগুলো বের করে দেবে। যেরকম 25-এর জন্য
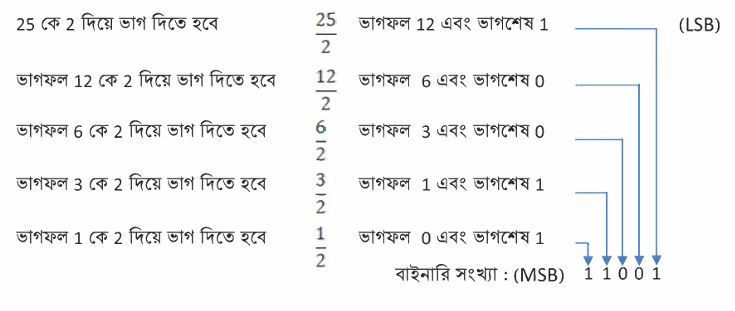
পদ্ধতিটা বুঝে গেলে আমরা সেটাকে আরো সংক্ষেপে লিখতে পারি। যেরকম 37 এর জন্য আমরা লিখব:
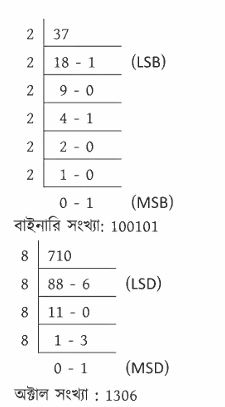
এই পদ্ধতিটি আমরা দশমিক থেকে অন্য যে কোনো ভিত্তিক সংখ্যায় রূপান্তর করার জন্যও ব্যবহার করতে পারি। শুধু 2-এর পরিবর্তে যে ভিত্তিক সংখ্যায় রূপান্তর করতে চাই সেই সংখ্যাটি দিয়ে ভাগ করতে হবে।
ডেসিমেল থেকে অক্টাল এখানে আমরা আগে দেখানো ডেসিমেল থেকে বাইনারি সংখ্যায় রূপান্তরের পদ্ধতিটি ব্যবহার করব, তবে অক্টাল সংখ্যার বেজ যেহেতু 8 তাই 2 দিয়ে ক্রমান্বয়ে ভাগ করার পরিবর্তে 8 দিয়ে ক্রমান্বয়ে ভাগ করা হবে। যেমন- 710 কে অক্টালে রূপান্তর করার জন্য লিখব:
অক্টাল থেকে বাইনারি অক্টাল সংখ্যার একটি বড় সুবিধা হচ্ছে যে, যেকোনো সংখ্যাকে খুব সহজে বাইনারিতে রূপান্তর করা যায়। অক্টাল সংখ্যার অঙ্কগুলো হচ্ছে 0,1,2,3,4,5,6 এবং 7 এবং এই প্রত্যেকটি সংখ্যাকে তিন বিট বাইনারি সংখ্যা হিসেবে প্রকাশ করা যায়।

এই রূপান্তরটি ব্যবহার করে যে কোনো অক্টাল সংখ্যাকে তার জন্য প্রযোজ্য তিনটি বাইনারি সংখ্যা দিয়ে প্রকাশ করলেই পুরো অক্টাল সংখ্যার বাইনারি রূপ বের হয়ে যাবে। যেমন:

তবে নিচের উদাহরণে সর্ব বামে দুটি 0 রয়েছে এবং সেই দুটো লেখার প্রয়োজন নেই। তাই-14538 = 11001010112
বাইনারি থেকে অক্টাল একই পদ্ধতির বিপরীত প্রক্রিয়া করে আমরা খুব সহজে যে কোনো বাইনারি সংখ্যাকে অক্টাল সংখ্যায় রূপান্তর করতে পারব। প্রথমে বাইনারি সংখ্যার অঙ্কগুলো তিনটি তিনটি করে ভাগ করে নিতে হবে। সর্ববামে যদি তিনটির কম অঙ্ক থাকে তাহলে এক বা দুইটি শূন্য বসিয়ে তিন অঙ্ক করে নিতে হবে। তারপর প্রতি তিনটি বাইনারি অঙ্কের জন্য নির্ধারিত অক্টাল সংখ্যাগুলো বসিয়ে নিতে হবে। যেমন:

এখানে তিনটি করে মেলানোর জন্য সর্ব বামে একটি বাড়তি শূন্য বসানো হয়েছে।
হেক্সাডেসিমেল থেকে ডেসিমেল হেক্সাডেসিমেল থেকে ডেসিমেলে রূপান্তর করার করার জন্য আমরা অঙ্কগুলোকে তাদের নির্দিষ্ট স্থানীয় মান দিয়ে গুণ করে একসাথে যোগ করে নেব। হেক্সাডেসিমেলের বেজ যেহেতু 16 তাই স্থানীয় মান হবে যথাক্রমে 160, 161, 162, 163 এরকম:
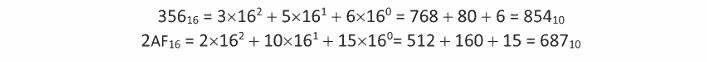
লক্ষ করতে হবে যে এখানে হেক্সাডেসিমেল A-এর পরিবর্তে 10 এবং F-এর পরিবর্তে 15 বসানো হয়েছে।
ডেসিমেল থেকে হেক্সাডেসিমেল এখানেও আমরা বাইনারি কিংবা অক্টাল সংখ্যার জন্য আগে দেখানো পদ্ধতিটি ব্যবহার করব। তবে বেজ যেহেতু 16 তাই 2 কিংবা 8 দিয়ে ক্রমান্বয়ে ভাগ করার পরিবর্তে 16 দিয়ে ক্রমান্বয়ে ভাগ করা হবে। ভাগশেষ যদি 10 কিংবা তার থেকে বেশি হয় তাহলে পরিচিত ডেসিমেল অংকের পরিবর্তে যথাক্রমে A, B, C, D, E এবং F লিখতে হবে। এই পদ্ধতিতে 7106 কে হেক্সাডেসিমেলে রূপান্তর করা হয়েছে। এখানে উল্লেখ্য, ভাগশেষ হিসেবে 12 সংখ্যার জন্য C এবং 11 সংখ্যার জন্য হেক্সাডেসিমেল প্রতীক B লেখা হয়েছে।
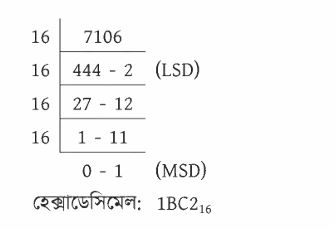
হেক্সাডেসিমেল থেকে বাইনারিঅক্টাল সংখ্যার বেলায় আমরা প্রত্যেকটি অক্টাল অঙ্কের জন্য তিন বিট বাইনারি সংখ্যা ব্যবহার করেছিলাম। হেক্সাডেসিমেলের জন্য প্রতিটি হেক্সাডেসিমেল অঙ্কের জন্য চার বিট বাইনারি সংখ্যা ব্যবহার করা হবে।

সর্ববামে 0 থাকলে সেগুলোকে রাখার প্রয়োজন নেই।বাইনারি থেকে হেক্সাডেসিমেলএখানেও আগের মতো বাইনারি সংখ্যাগুলোকে চারটি সমন্বয় করে ভাগ করে নিতে হবে। সর্ব বামে যদি চারটির কম বাইনারি অঙ্ক থাকে তাহলে সেখানে প্রয়োজনীয় সংখ্যক 0 বসিয়ে চারটির গ্রুপ করে নিতে হবে। তারপর প্রতি চারটি বাইনারি সংখ্যার জন্য নির্ধারিত হেক্সাডেসিমেল সংখ্যাটি বসিয়ে দিতে হবে।যেরকম:
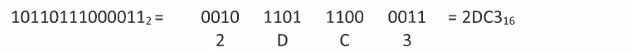
হেক্সাডেসিমেলে যেহেতু চারটি বাইনারি অঙ্ক একটি হেক্সাডেসিমেল অঙ্ক দিয়ে প্রতিস্থাপন হয় তাই অনেক বড় বাইনারি সংখ্যা লেখার জন্য হেক্সা অথবা অক্টাল সংখ্যা ব্যবহার করা হয়।সমস্যা: হেক্সাডেসিমেল সংখ্যা 38 থেকে শুরু করে পরবর্তী 25টি সংখ্যা লিখ। হেক্সাডেসিমেল 38-এর দশমিক মান কত?
হেক্সাডেসিমেল থেকে অক্টাল কিংবা অক্টাল থেকে হেক্সাডেসিমেলে রূপান্তর করার সবচেয়ে সহজ নিয়ম হচ্ছে, প্রথমে বাইনারিতে রূপান্তর করে নেয়া। তারপর হেক্সাডেসিমেলের জন্য চারটি করে এবং অক্টালের জন্য তিনটি করে বাইনারি অঙ্ক নিয়ে তাদের জন্য নির্ধারিত হেক্সাডেসিমেল অথবা অক্টাল সংখ্যাগুলো বেছে নেয়া। যেমন:
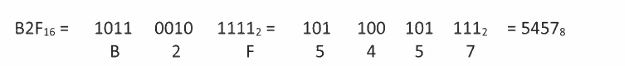
এখানে B2F16 কে অক্টালে রূপান্তর করার জন্য প্রথমে সংখ্যাটির তিনটি হেক্সাডেসিমেল অঙ্কের জন্য নির্ধারিত চারটি করে বাইনারি অঙ্ক ব্যবহার করে মোট 12টি বাইনারি অঙ্কে রূপান্তর করা হয়েছে। তারপর এই 12টি বাইনারি অঙ্ককে তিনটি করে মোট 4টি গ্রুপে ভাগ করা হয়েছে। এবারে প্রতি গ্রুপের জন্য নির্ধারিত অক্টাল অঙ্কগুলো বসিয়ে 54578 পাওয়া গেছে। এভাবে তিনটি অঙ্কের গ্রুপ করার সময় প্রয়োজন হলে সর্ব বামের গ্রুপটিতে একটি বা দুইটি বাড়তি 0 বসানো যেতে পারে।