আমরা এবারে লজিক গেট দিয়ে তৈরি করা আরো একটি ডিজিটাল সার্কিটের কথা বলব যেটি বাইনারি সংখ্যা যোগ করতে পারে। আমরা ইতোমধ্যে জেনে গেছি যে সঠিকভাবে বাইনারি সংখ্যা যোগ করতে পারলেই প্রয়োজনে সেই একই সার্কিট ব্যবহার করে বিয়োগ, গুণ এবং ভাগ করতে পারব।
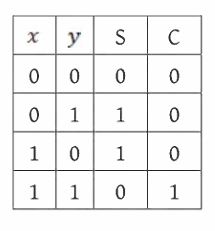
X-OR লজিক গেটটি আলোচনা করার সময় আমরা বাইনারি যোগ 1+1=10 সংখ্যাটিতে বলেছিলাম এর মাঝে ডান পাশের বিটটি যোগফল এবং বাম পাশের (হাতে থাকা) বিটটি ক্যারি (carry)। যোগফলের বিটটি X-OR গেট দিয়ে পাওয়া যায় কিন্তু ক্যারি বিটটি কীভাবে পাওয়া যায় সেটি তখন আলোচনা করা হয়নি। সেটি খুবই সহজ একটি AND গেট দিয়ে পাওয়া যেতে পারে। কাজেই আমরা একটি বিটের সাথে অন্য একটি বিটের বাইনারি যোগ নিচের সার্কিট দিয়ে পেতে পারি (চিত্র 3.18):
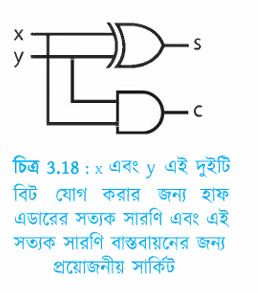
এই ধরনের সার্কিটের নাম হচ্ছে হাফ অ্যাডার, কারণ এটি পূর্ণাঙ্গ বাইনারি যোগের সার্কিট নয়, এটি আংশিকভাবে যোগ করতে পারে। আগের ধাপ থেকে ক্যারি বিট হিসেবে 1 চলে এলে তখন যোগ করতে পারে না। প্রকৃত বাইনারি যোগে দুটি বিট যোগ করতে হলেও মাঝে মাঝেই এর আগের দুটি বিটের যোগ থেকে ক্যারি বিট চলে আসে, তখন দুইটি নয়, তিনটি বিট যোগ করার প্রয়োজন হতে পারে। নিচে দুটি বাইনারি সংখ্যার যোগফল দেখানো হয়েছে।
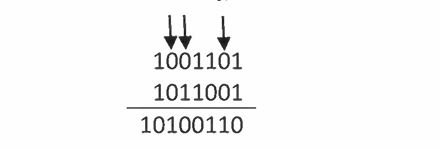
যদিও দুটি করে বিট যোগ করা হয়েছে কিন্তু তীর চিহ্ন দি দেখানো বিট দুটির বেলায় আগের ধাপ থেকে 1 বিটটি এসেছে বলে আসলে তিনটি বিট যোগ করা হয়েছে। আমরা অন্যভাবেও বলতে পারি, প্রতিবারই আমরা তিনটি বিট যোগ করেছে, কিন্তু অন্য ধাপগুলোতে ক্যারি বিটের মান ছিল 0। কাজেই এবারে আমরা x, y এবং CIN, এই তিনটি ইনপুটের জন্য ট্রুথ টেবিলটি লিখে ফেলতে পারি।
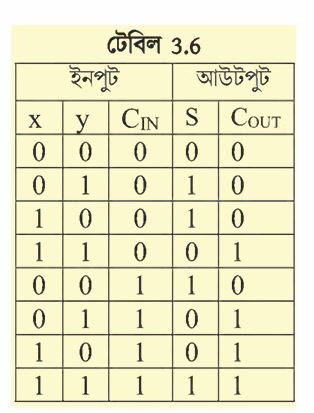
এখানে x, y হচ্ছে বাইনারি যোগের প্রদত্ত সংখ্যার বিট এবং CIN হচ্ছে আগের ধাপ থেকে আসরা ক্যারি বিটের মান। ট্রুথ টেবিলে আউটপুট দুটি, S এবং COUT। S হচ্ছে দুটি বিটের যোগফল, COUT হচ্ছে ক্যারি বিট যেটি পরের ধাপে CIN হিসেবে যুক্ত।
ট্রুথ টেবিলের দিকে তাকিয়ে আমরা দেখতে পাচ্ছি x, y এবং CIN এর সম্ভাব্য আটটি ভিন্ন ভিন্ন ইনপুটের এর ভেতর চারটি ক্ষেত্রে যোগফল (S) এবং চারটি ক্ষেত্রে ক্যারি (COUT) আউটপুটের মান 1 হতে হবে। ডিকোডারের বেলায় আমরা যেভাবে AND গেটের আউটপুট 1 পাওয়ার জন্য NOT গেট দিয়ে ইনপুট পরিবর্তন করেছিলাম, এখানেও আমরা হুবহু একই পদ্ধতি গ্রহণ করতে পারি। 3.19 চিত্রে সেভাবে সার্কিটটি এঁকে দেখানো হলো।
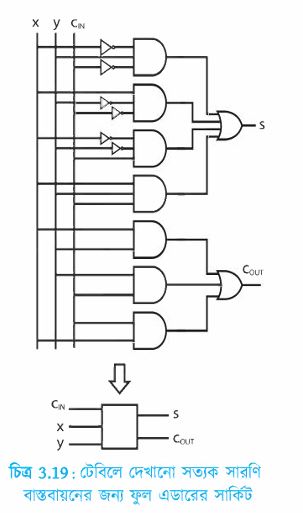
আমাদের আউটপুট দুটি (S এবং COUT) পাওয়ার জন্য AND গেটগুলোর OR গেট দিয়ে একত্র করে নেয়া হয়েছে। তবে তোমরা একটু অবাক হয়ে ভাবতে পার, S এবং COUT দুটির লজিক একই ধরনের থাকার পরও COUT এর জন্য সার্কিটটি তুলনামূলক ভাবে সহজ কেন? মাত্র তিনটি দুই ইনপুট AND গেট দিয়ে কীভাবে আমরা সঠিক আউটপুট পেয়ে গেলাম?
S এর বেলায় 1 আউটপুটের জন্য INPUT এর মান হতে হবে এরকম:
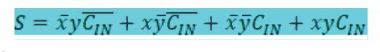
একইভাবে ক্যারি আউটের জন্য COUT এর মান হতে হবে এরকম:
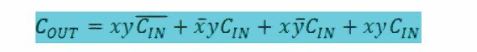
কিন্তু এটাকে সহজ করে এভাবে লেখা সম্ভব। কীভাবে সম্ভব তার উত্তরটি নিচের উদাহরণে ব্যাখ্যা করা হয়েছে।
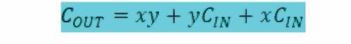
উদাহরণ: S এর জন্য আউটপুটটি মৌলিক গেট দিয়ে আরও সরল করা সম্ভব না। তবে COUT এর সমীকরণটি আরও সরল করা সম্ভব। তোমরা কি আরও সরল করে দেখাতে পারবে?
উত্তর: যেহেতু A+A=A, তাই আমরা সর্বশেষ টার্ম xyCIN টি অন্য তিনটি টার্মের প্রত্যেকটির সাথে যোগ করতে পারি:
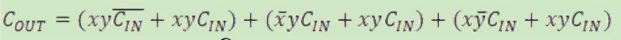
দেখতে পাচ্ছ পুরো সার্কিটটি অনেক সরল হয়ে গেছে, কিন্তু এটি সঠিক আউটপুট দেবে, ইচ্ছা করলে সেটি পরীক্ষা করে দেখতে পার।
দুটি বিট যোগ করার এই সার্কিটটিকে ফুল অ্যাডার বলে। যেকোনো সত্যকার কাজের সার্কিটে অনেক বিট যোগ করতে হয়, কিন্তু প্রত্যেকটি বিটের জন্য যেন এই পুরো সার্কিটটি আঁকাতে না হয় সেজন্য আমরা পুরো সার্কিটটিকে একটা ব্লক ডায়াগ্রাম দিয়ে দেখিয়েছি, এখানে শুধু ইনপুট এবং আউটপুট লাইনগুলো দেখানো হয়েছে। চার বিটের একটি বাইনারি যোগের জন্য কীভাবে চারটি ফুল ডার সার্কিট যোগ করতে হবে সেটি ব্লক ডায়াগ্রাম গুলো যুক্ত করে দেখানো হলো (চিত্র 3.20)।
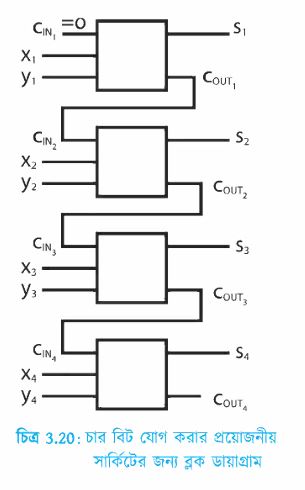
লক্ষ কর, প্রথম ব্লক ডায়াগ্রামে CIN1=0 কারণ প্রথম দুটি বিট যোগ করার সময় আগের কোনো ধাপ থেকে কিছু CIN আসা সম্ভব নয়। উল্লেখ্য যে, চার বিট যোগ করতে হলে যোগফল সঠিকভাবে দেখাতে হলে কিন্তু সর্বশেষ COUT এর জন্য পঞ্চম বিট প্রয়োজন হয়।