আমাদের প্রচলিত এলজেবরার মতোই বুলিয়ান এলজেবরার বেশ কিছু উপপাদ্য রয়েছে। এর মাঝে গুরুত্বপূর্ণ কয়েকটি নিচে দেখানো হলো। বুলিয়ান এলজেবরা যেহেতু {0,1} সেট দিয়ে তৈরি তাই চলকের (Variable) মান একবার 0 এবং আরেকবার 1 বসিয়ে এই উপ পাদ্যগুলো খুবই সহজেই প্রমাণ করা যায়।
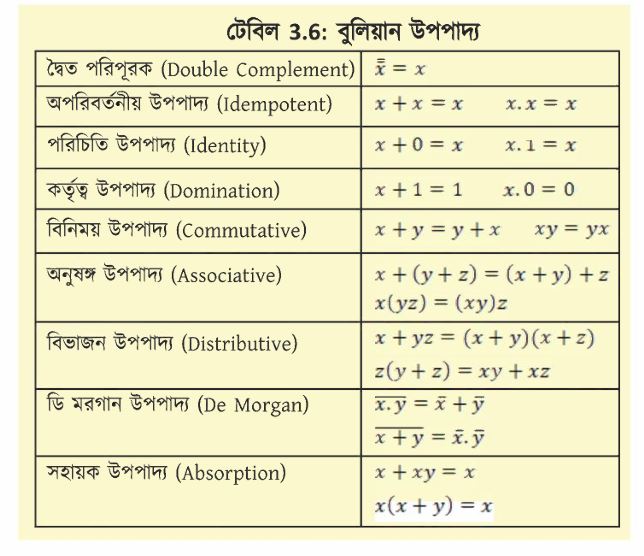
এখানে বেশ কিছু উপপাদ্য আমাদের পরিচিত এলজেবরার সাথে সঙ্গতিপূর্ণ আবার বেশ কিছু উপপাদ্যের পরিচিত উপপাদ্যের সাথে মিল নেই।

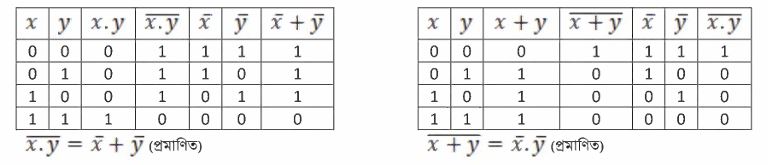
উদাহরণ: ডি মরগানের উপপাদ্য দুটি প্রতি ক্ষেত্রের জন্য মান বসিয়ে প্রমাণ কর।
উত্তর: এখানে যেহেতু x এবং y দুটি চলক রয়েছে, দুটিরই মান হওয়া সম্ভব ০ এবং ১ কাজেই সর্বমোট ২২ বা চারটি। ভিন্ন মান হওয়া সম্ভব। প্রত্যেকটির জন্য আলাদাভাবে লেখা যেতে পারে।

আমাদের পরিচিত সাধারণ এলজেবরায় আমরা যেরকম বেশ কিছু চলক ব্যবহার করে অন্য আরেকটি বড় এক্সপ্রেশন তৈরি করতে পারি, বুলিয়ান এলজেবরার বেলাতেও সেটা সত্যি। সাধারণ এলজেবরার মতো বুলিয়ান এলজেবরাতেও আমরা বুলিয়ান উপ পাদ্যগুলো ব্যবহার করে সেগুলো অনেক সরল করে ফেলতে পারি। যেমন ধরা যাক x, y এবং z এই তিনটি চলক ব্যবহার করে নিচের এক্সপ্রেশনটি লেখা হয়েছে:
xyz + xy + x
এটাকে আমরা এভাবে সরল রূপ দিতে পারি:
xyz + xy + z = xy(z+1) + x = xy + x = x(y+1) = x
এটাকে সরল করার জন্য আমরা domination উপপাদ্য z + 1 = 1 এবং y + 1 = 1 ব্যবহার করেছি।

আমরা যখন ডিজিটাল ইলেকট্রনিক্সের শুরুতে নানা ধরনের গেট নিয়ে আলোচনা করব তখন দেখব বুলিয়ান এলজেবরায় এভাবে একটি বড় এবং জটিল এক্সপ্রেশনকে সরল করতে পারলে একটি জটিল সার্কিটকে অনেক ছোট করে ফেলা যায়।